感受器神经元在根据环境变化（适应性）的能力上取代了人造传感器，但其基本机制仍然是感受神经科学中的传统挑战。为了研究这种适应过程，宋卓异博士构建了感受受体的多尺度计算模型，旨在将信号传导动力学从分子到系统层面联系起来。

       在6月12日的讲座中，来自复旦大学类脑智能科学与技术研究院（ISTBI）青年研究员，宋卓异博士介绍了多尺度建模方法，以及所揭示的一种随机的自适应采样机制。该讲座主要分为感知系统自适应与随机自适应采样机制两部分。在开始之前，先让我们欣赏一下宋卓异博士的代表作成果吧。

 

代表性成果1：揭示光感受器感知大范围光强变化的自适应机制

照相机vs人眼

       照相机光圈小时，进光量小，能看到亮处的背景，但暗处的背景细节会丢失；相反，照相机光圈大时，进光量多，能看到暗处的背景，亮处的背景会引起系统（即芯片）的饱和，从而导致亮处细节信息丢失。

       然而人眼并不会有这种问题。那么，动物是如何实现这种大范围的、动态的感光范围呢？这种思想能否用于仿生眼的构建呢？

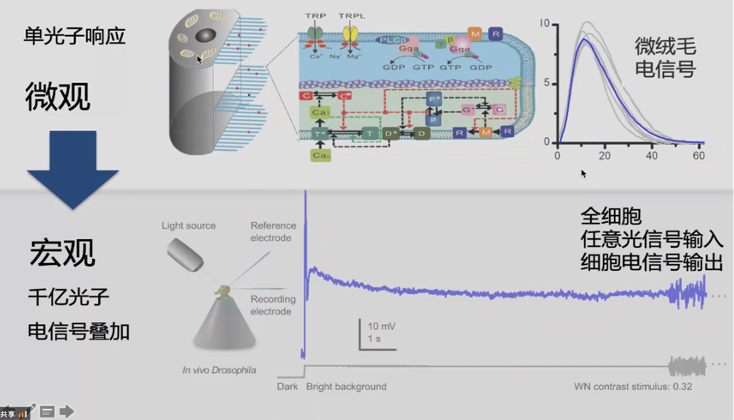
        解决方案：构造从微观到宏观的光感受器仿生模型。

       图中左上角为果蝇的光感受器的细胞（可感受单光子信号），右上角为一个单光子所产生的QB（Quantum Bump）的电流信号。在整合电流信号时，一个光子到一个Quantum Bump电荷间的放大倍数是6000。这样的机制，就可以让动物在极暗光的环境下看到物体，这是现在的照相机所做不到的。从宏观角度来看，在千亿数量的光子情况下，仿生神经元模型依然能够正常运作。

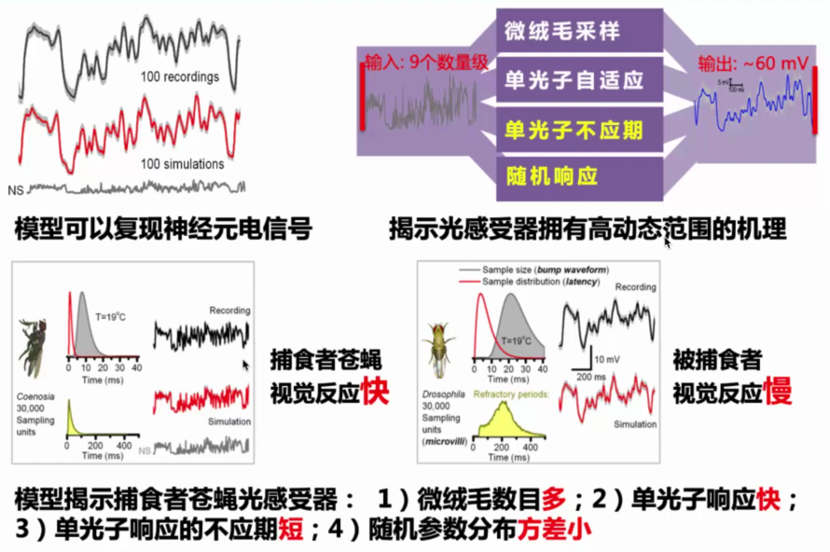
       上图的左上角图中底部NS为光强序列，黑线为实验测的光感受器的响应，红线为模型的仿真结果。可以看到，模型的复现结果非常好，而且该模型无需进行参数调整。现在，让我们打开这个白箱模型，来进一步看其内部的运作机制。该模型是如何解释神经元拥有大的高动态感光范围。这里我们提出了四个机制（右上角图中，黄字为新提出的创新机制），具体细节见本文硬件层面分析。下方的两个子图中表示了捕食者苍蝇与被捕食苍蝇的光感受器之间的区别：捕食者苍蝇第一层感光神经元的视觉反应比被捕食苍蝇的反应要快，这与其生存压力息息相关。

 

代表性成果2：光感受器微跳视机制帮助复眼抵消运动模糊

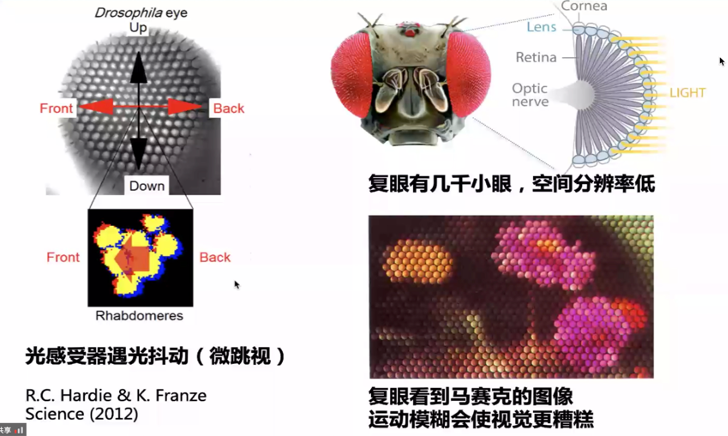
       光感受器遇光会发生抖动（微跳视）的现象，即也拥有压力感知器的特性。这令人惊讶！因为这种抖动现象通常是在压力感知器或听力感知器上存在。2012年Hardie和Franze初次在光感受器上发现微跳视现象，其成果发表在Science上。但是这种微跳视现象对视觉产生什么样的影响呢？我们知道，拍照时照相机的抖动会造成糊片；那么本来果蝇复眼看到的就是马赛克图像，如果再加上感受器的抖动现象，这不会让复眼看到的图像更糟糕吗？当然实验证实，果蝇拥有高分辨率的视觉行为。那么微跳视到底是怎么样影响视觉的呢？

微跳视可以调制光信号的变化

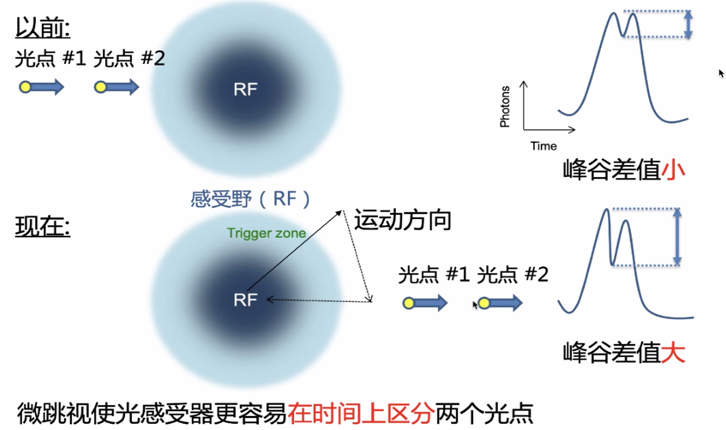
       图中上排显示，当两个光点经过感受野时，峰谷差值小，这会使果蝇把经过的两个光点当成一个光点。图中下排显示，微跳视使感受野移动，使得峰谷差值变大，从而果蝇能更容易的区分两个光点，增加空间分辨率。

Part1 感知系统自适应（sensory adaptation）：

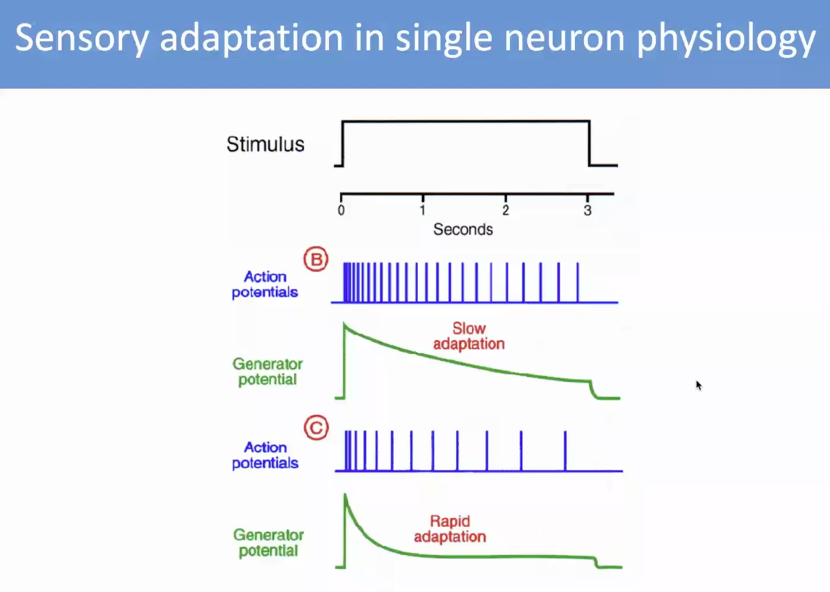
        神经元具有自适应性，即不断的刺激输入的情况下，神经元放电输出会随时间减少。那么如何理解这种自适应，它是如何产生的？

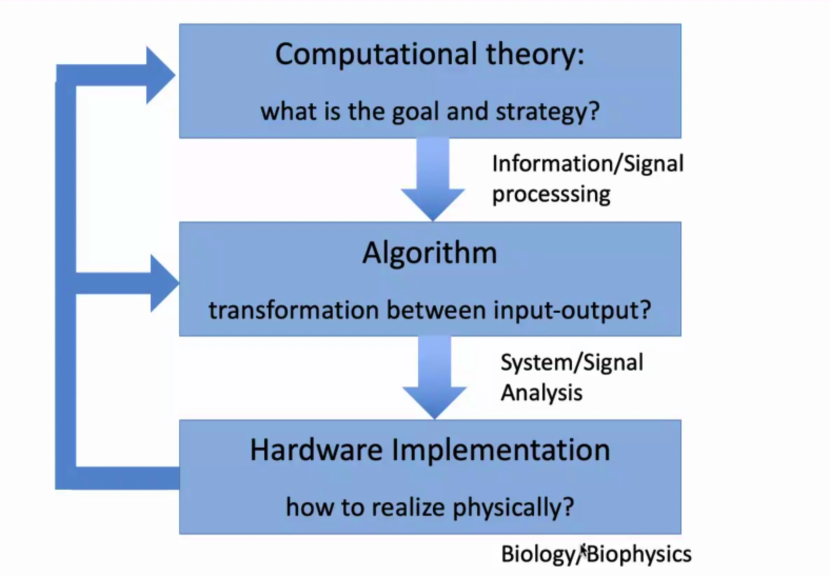
       根据Marr’s three levels of analysis（三级计算理论分析框架），即一个系统需要从以下三个层次进行研究：

1.计算理论（计算目标是什么？）

2. 算法（如何设计算法，来实现输入输出映射关系？）

3. 硬件实现（芯片或生物学系统如何物理实现？）

       对于光感受器系统，我们需要从以上三个层面来理解系统。传统的方式是自顶到下进行分析。即首先明确：感知自适应的计算目标是什么，是什么原则决定着感知自适应。

       物理学家们过去曾对此提出三种不同的理论：1）需要把能量提供给新颖的事件，自适应的计算目标是为了在新颖事件上保持注意力；2）不变的信号不含有信息，自适应是为了移除冗余信息；3）自适应是为了最大化神经元所刻画的信息量。

       下面我们集中于第三个理论，即信息最大化理论（information maximization theory），展开讨论。

       光信号在大脑中处理过程的框架如下：

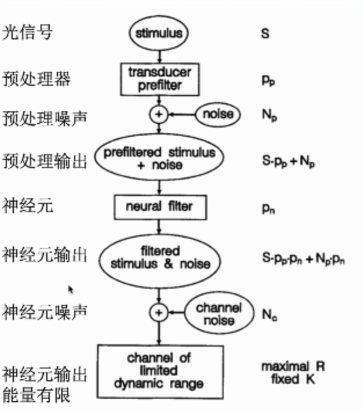
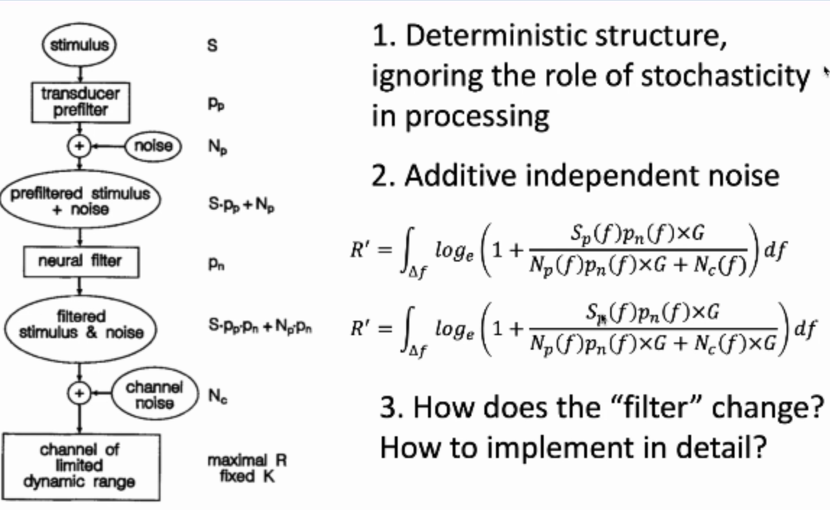
       如何最大化得到输出的信息？即在输出范围（dynamic range K）有限的情况下，如何设计Pn(neural filter神经元)使R（信息量）最大。

       下面是基于信息最大化理论的两种预测：

       预测一：假设channel noise与neural filter相互独立，可在neural filter上增加G增益，使得R'大于R，如下图所示。（Brenner et al. 2020）

       预测二：neural filter的自适应滤波性质。如下图所示，高信噪比情况下，neural filter的频谱特性与输入谱成倒数关系，具有高通或带通的滤波器特性；而低信噪比情况下，neural filter的频谱特性与输入谱成正比关系，具有低通的滤波器特性。（Sharpee et al.证明，自适应滤波有利于视觉皮层的信息传输。）

       这个框架的局限性：

1.自适应滤波为确定性过程，忽略了神经元本身具有随机性的量纲。

2.假设中channel noise与neural filter是独立关系，才能最大化信息，但如果Pn和G是相关关系时，在Pn上添加G，就相当于在Nc上添加G，就会相互抵消，导致R没有增大。

3.没有说明filter低通到高通变化过程以及具体机制。

       在从三级计算理论框架自顶向下的研究中我们遇到了局限性，那么自底向上的研究能不能突破这些局限性呢？

       物理学家Yakov Frenkel认为:“一个好的复杂系统的理论模型，需要突出其中重要的特点而忽略不重要的细节。”但是在研究的时候，我们很难知道哪个是重点哪个不是重点。因此，我们采用自底向上的方法先去研究现象，看能否在其中找到重要与不重要的信息。这里需要一个系统让我们能够采用自底向上的模式，这就需要系统满足自适应和足够的背景知识让我们来构建模型两个条件。我们最后选择了果蝇光感受器，因为它具有强大的光自适应能力，一个神经元可处理任意光强。过去的研究工作主要集中在两个领域，其中物理学家通过自顶向下的方式研究，通常提出计算理论来预测神经元的机制，而生物学家通过做各种实验来研究生物物理机制。宋卓异博士提出构建全细胞（whole-cell）模型（即生物物理模型，从基因分子层级开始搭建系统直到搭建到细胞模型并将映射出输入输出的关系为止）来将两个领域的工作联系起来，填补这两个领域之间的空白。

硬件层面分析：

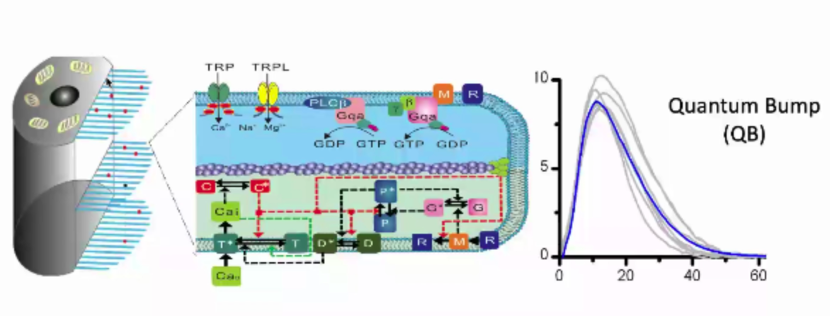
      果蝇光感受器的模型：左图为一个胞体（非感光部分）与微绒毛（感光部分，数量为三万个），中间图表示微绒毛的分子反应网络，将光子转导为电流响应（右图，Quantum Bump）。主要针对单细胞对于单光子相应的过程来构建分子反应链，这并不是系统模型，不能模拟细胞在持续响应光子输入情况下的输出。

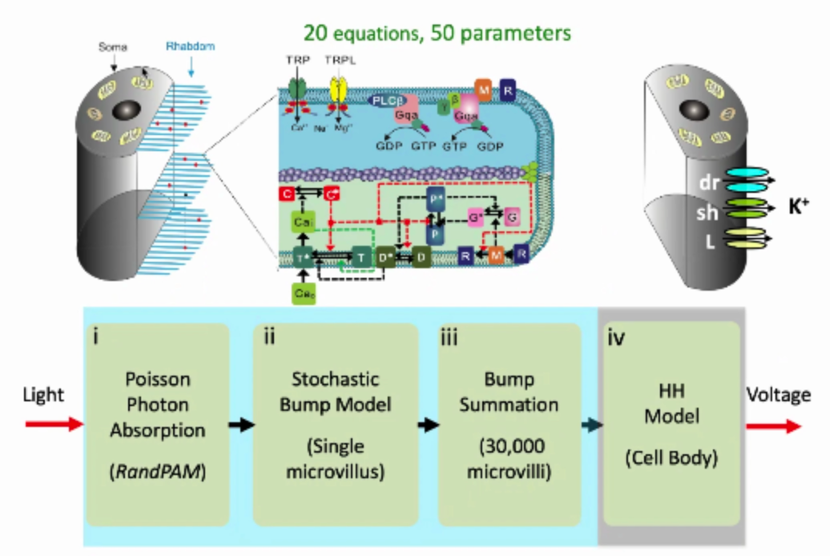
       上图为宋卓异博士设计的一套模型系统，能够将整个光感受器的输入映射到电压信号的输出，共分4个环节：

1.三万个微绒毛吸收光子的过程。

2.对于每个微绒毛，都有一系列的分子反应链的模型来转导光子的能量。

3.仿真三万个微绒毛所产生的光电流并集成起来输入到胞体上。

4.使用Hodgkin-Huxley模型模拟胞体上的钾离子通道的动态特性来产生电压信号。

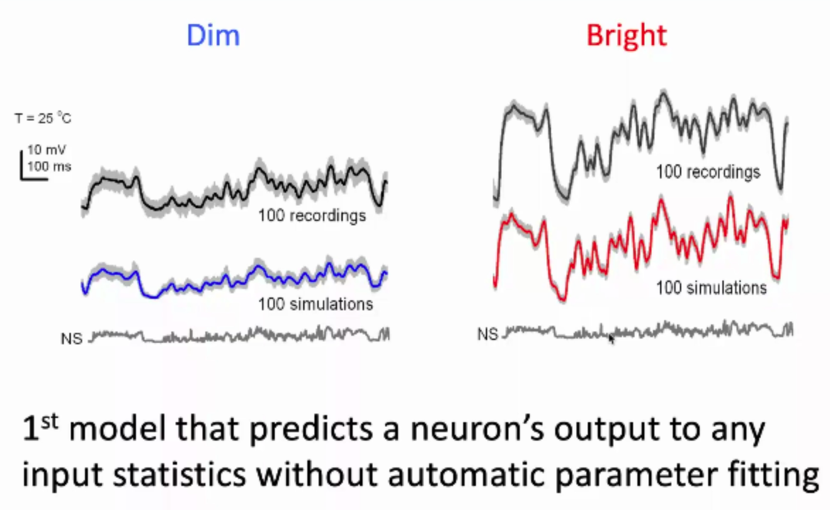
       图中显示了在不同的光强序列、暗光、亮光条件下，真实神经元的响应结果与模型仿真结果十分接近。而且模型具有无需调参，扩展性好的优点。

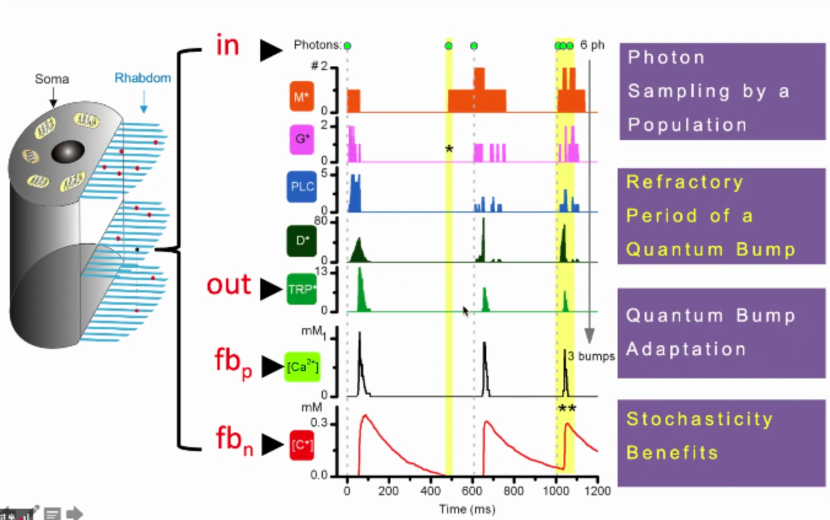
       在具有一个比较好的模型的情况下，我们可以打开模型，向三级计算理论分析中的上面两层前进。首先我们对计算理论分析的最下层hardware implementation进行分析。模型可以响应一个光子输入序列，这是之前业内没做过也是实验中做不到的，因为微绒毛太小，不能够测得单个微绒毛对于光子序列的响应，只有在计算机仿真里可以看到每个微绒毛对光子响应序列的反应动态。分析提出了使光感受器有大范围感光能力的4个机制：

1.大量微绒毛来感光。

2.单光子反应的不应期。

3.单光子响应，暗光响应大，亮光响应小，Quantum Bump(QB) Adaptation亮光暗光反应相差可达50倍。

4.在反应过程中，内部为随机机制。

       其中红色的两项机制为宋博士提出的新的机制。传统观点认为这两点都不利于信息编码，反应不应期会丢失信息，随机过程会降低信噪比。然而，这并不全面，这两点对于系统的自适应是十分有益的。

算法层面分析：    

       Jhon Von Neumann认为参数个数多的复杂模型拟合数据好并不能说明什么，所以简化模型更能方便研究其内部机制而且有利于构建大型仿真系统。根据四个机制简化模型，减少原参数数量（50个）到4个关键参数，即绒毛的数量，光子到来到响应的延迟（Delay），Quantum Bump(QB)形状，两个QB之间的时间间隔即不应期。     

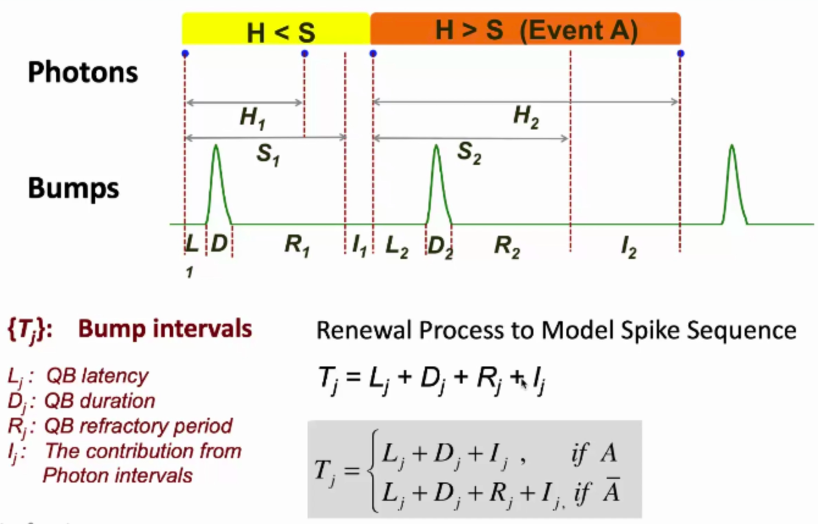
       上图表示反应不应期分为两种情况：光子在不应期期间到来，光子会被丢失；光子在不应期之后到来，会形成QB。

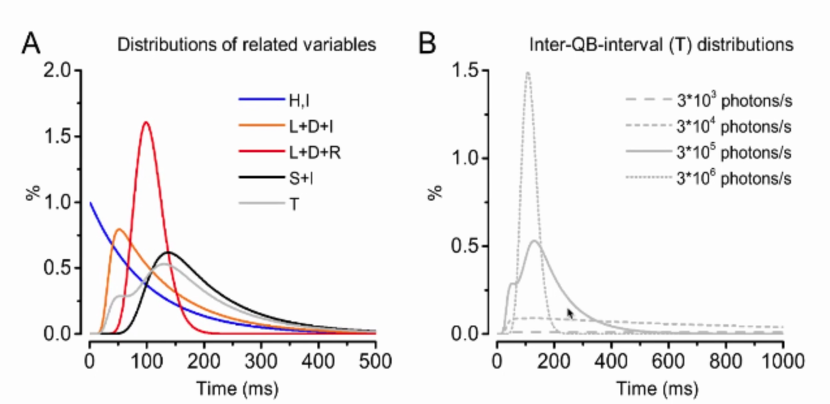
       图A为不同随机量的分布，图B为在不同的光强条件下，QB的Interval有自适应的调节，即在暗光条件下，更趋向于long tail的分布，在亮光条件下更趋向于不应期的分布。

Gain control by refractory sampling分析：

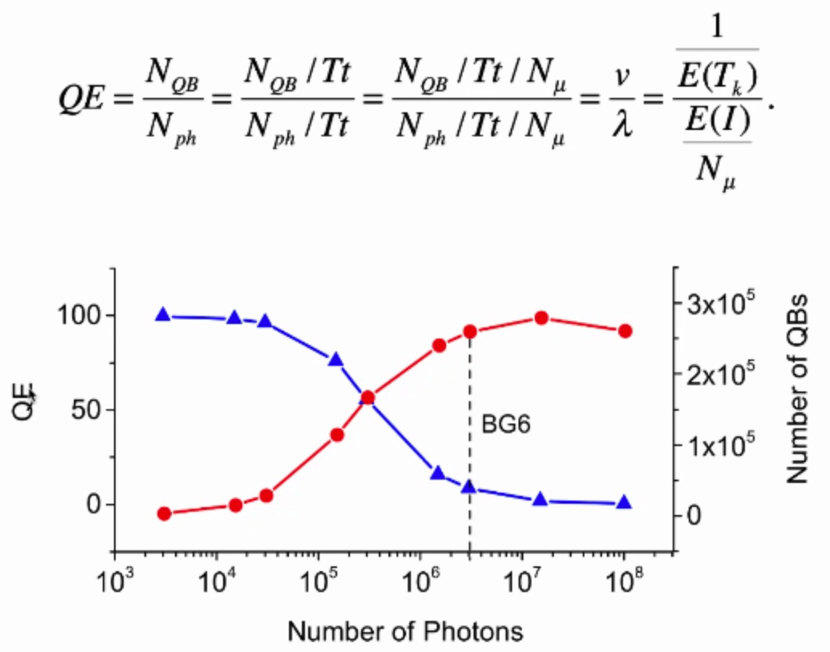
       QE(quantum efficiency)为光子形成QB的比例。由于这种bump interval分布的自适应，使得系统拥有自动增益控制机制：在暗光条件下，每个光子都可产生QB，所以QE为100%。而强光条件下，光子会通过不应期丢掉，QE会下降（可降至1%）。

Adaptive filtering分析：

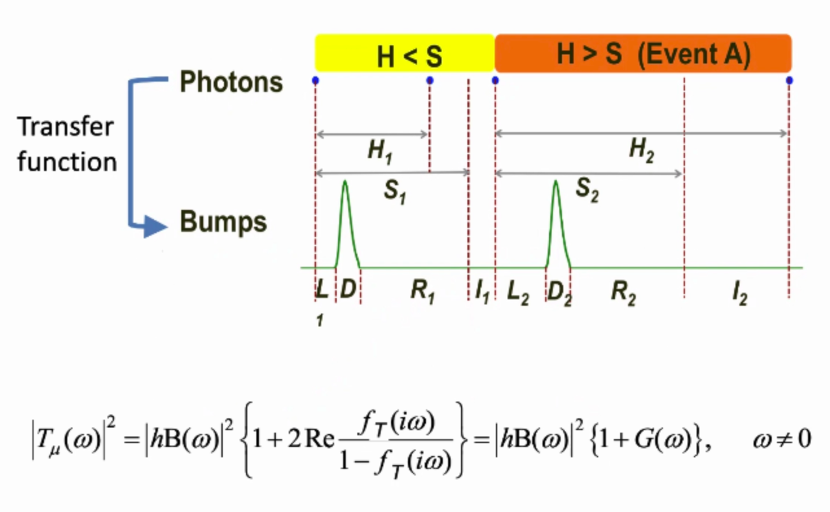
       通过分析transfer function，由于随机的反应不应期得出adaptive filtering的机制：在暗光条件下，图中标记叉号的大括号中反应不应期的那项为0，即大括号中只剩下1，所以transfer function为低通，主要由QB频谱决定。在亮光条件下，反应不应期不为0，所以具有带通性质。     

       这样也就复现了之前信息最大化的两个预测，先前也提到了理论框架的局限性，现在来看看该模型是否克服局限性：

1.没有假设noise和filter是否独立，无论独立与否都可产生自适应性。

2.通过refractory（不应期） sampling来解释了高通与低通转换机制。

3.对于先前忽略随机性的局限性，提出了随机性对于信号处理的重要性。

不应期的随机性分析：

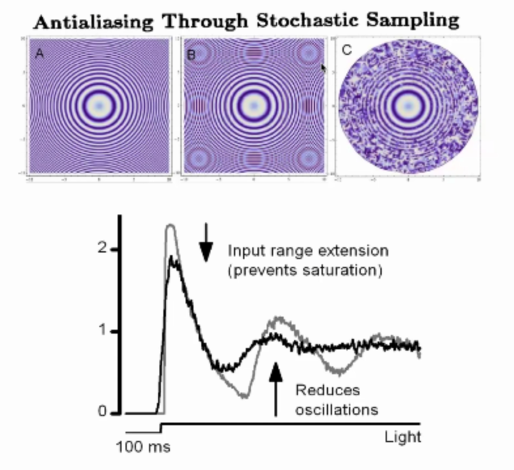
       根据奈奎斯特定理（Nyquist's Theorem），还原图像，采样频率需大于2倍的原频率，采样的信号才不会失真。采样频率低于原频率2倍时，会出现图B中的圆圈即为混叠效应也称为振铃效应。随机采样可以消除振铃效应，不过与噪声要有权衡。在视觉上，噪声可以通过平均消除，不过在感受器上形成的振铃效应是无法消除的。在时间上来也存在振铃效应问题（下图）。随机性的不应期（黑线）不容易产生震荡，然而确定性的不应期（灰线）容易产生震荡（类似于振铃效应的圆圈）。

自然界物种的自适应分析：

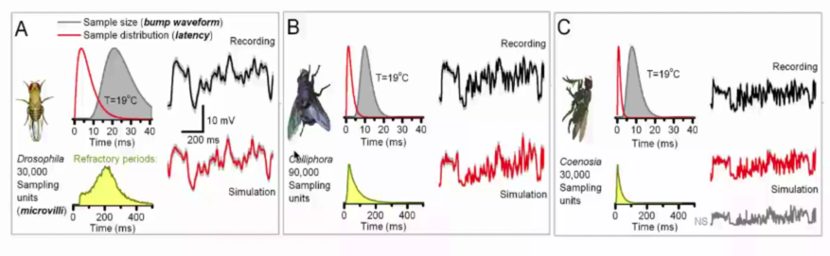
       捕食苍蝇比被捕食苍蝇的神经元反应要快，响应快三倍，具有以下几种机制：

1. 单光子响应QB窄（图中红色曲线，显示捕食者苍蝇QB分布比被捕食者苍蝇窄）。

2. 不应期分布窄（图中黄色区域，显示捕食者苍蝇不应期的分布比被捕食者苍蝇窄）。

3. 微绒毛数量多（捕食者苍蝇拥有9万个微绒毛，而被捕食者苍蝇只拥有3万个）。

Part 1 总结：

1. 构建全细胞模型，可以把神经元的输入与输出都映射出来。

2. 有2个创新发现，亚细胞反应不应期可以作为强大的自动增益控制以及自适应的filtering机制；随机采样有利于应对信号处理的抗混叠。

3. 四个随机自适应采样机制也解释了自然界不同物种之间的神经元响应的不同特性。

 

Part 2 随机自适应采样机制:

       先前提到模型解决了理论框架所存在的3个局限性，不过没有说明到底是什么样的刺激可以让神经元编码信息最大化。

       从传统的框架来分析，如何设计Sp来让R最大化。通过信息论可以得到一定是高斯白噪声来让Sp最大化，因为高斯白噪声是一定的带宽下含信息量最大的信号。但是生物学家（Rleke et al. 1995）通过实验得出前端感知的神经元并不是对高斯白噪声响应最强烈而是对自然信号响应最强烈（是高斯白噪声的2到6倍）。

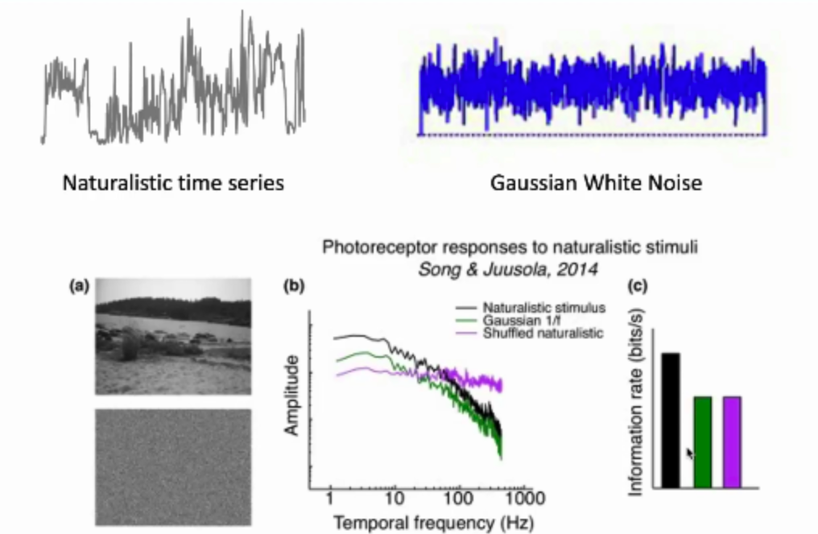
       然而一直没有机理解释为什么对自然信号的响应更强烈，直到宋卓异博士使用模型系统解释了其中的原因（Song & Juusola，2014）。使用不同的输入信号来刺激模型，图（c）中显示神经元可以对自然信号编码更多的信息。这是因为在自然光信号中，暗光信号附近很大概率还是暗光信号（而高斯白噪声相邻两点是不相关的），在连续的暗光信号时期，系统内部的微绒毛更容易从反应不应期之中恢复过来，从而采样更多的光子，编码更多信息。这也说明了光感受器对于变化的光强序列处理能力很强。对于动物来说，它们可以利用时空相关性来进行信息编码。那么到底是什么样的信号才能驱动光感受器呢？

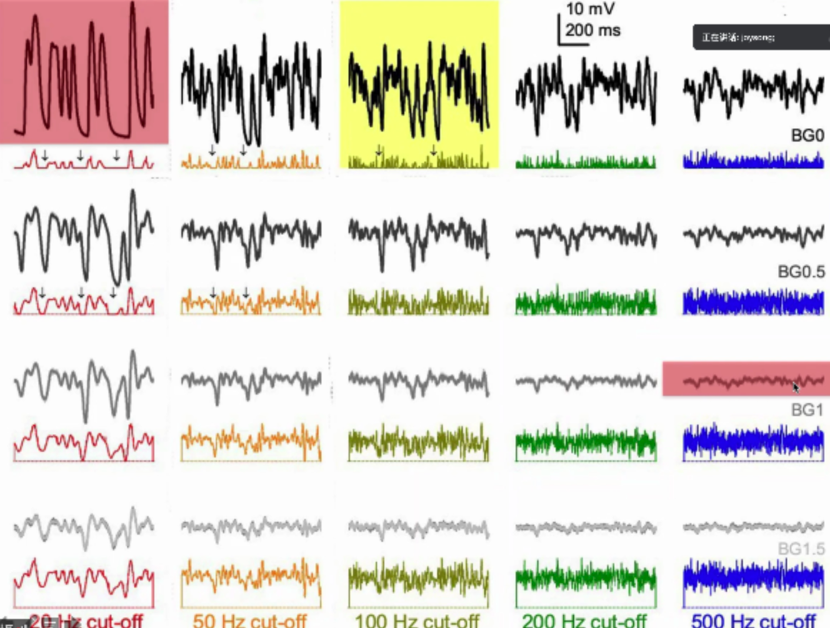
       于是我们设计了各种不同频段高斯白噪声以及pink noise等。图中黑色线为输出，彩色线为输入。在红色区域的两段对比可以看到，感受器对于高斯白噪声（右下角红色区域）反应不强，而对于五指山似(burst)的输入（左上角红色区域）反应强烈。那么动物是如何与环境互动来获得五指山一样的信号呢？

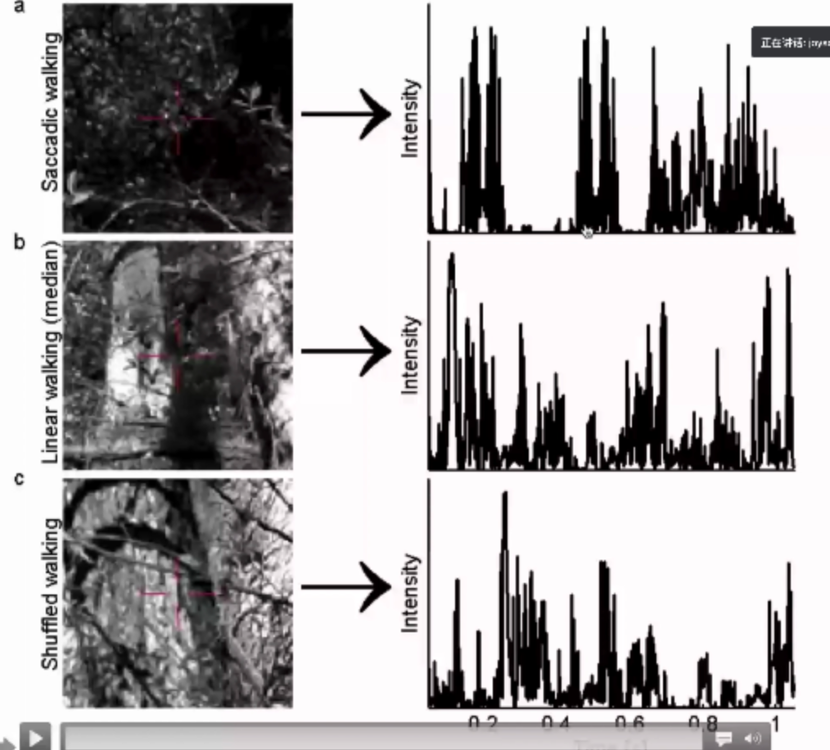
       通过对比动物三种不同的方式saccadic walking，linear walking, shuffled walking，发现saccadic walking可以产生burst形状的信号。其中大片暗光的视觉区域，可以使系统更容易地从不应期中恢复过来，从而编码更多信息。这就说明动物是可以通过自身行为、跟环境互动来调制光信号，来进行感知。

 

最后用Marr的三级计算理论分析来总结讲座：

1. Hardware Implementation Level：全细胞模型给出了生物物理的机制。

2. Algorithm Level：全细胞模型的研究设计了算法。

3. Computational theory Level：随机自适应采样理论，弥补了传统理论的不足，可能是神经信息编码最优采样方法之一。同时我们也期待新理论的出现。

 

 

Reference:

[1] Hardie, R. C., & Franze, K. (2012). Photomechanical responses in Drosophila photoreceptors. Science, 338(6104), 260-263.

[2] Brenner, N., Bialek, W., & Van Steveninck, R. D. R. (2000). Adaptive rescaling maximizes information transmission. Neuron, 26(3), 695-702.

[3] Sharpee, T. O., Sugihara, H., Kurgansky, A. V., Rebrik, S. P., Stryker, M. P., & Miller, K. D. (2006). Adaptive filtering enhances information transmission in visual cortex. Nature, 439(7079), 936-942.

[4] Song, Z., & Juusola, M. (2014). Refractory sampling links efficiency and costs of sensory encoding to stimulus statistics. Journal of Neuroscience, 34(21), 7216-7237.

[5] Rieke, F., Bodnar, D. A., & Bialek, W. (1995). Naturalistic stimuli increase the rate and efficiency of information transmission by primary auditory afferents. Proceedings of the Royal Society of London. Series B: Biological Sciences, 262(1365), 259-265.

 

文中图片来源：宋卓异博士讲座截图。

欢迎感兴趣的同学与宋卓异老师联系。宋老师接收博士、硕士、RA申请。

联系方式为songzhuoyi@fudan.edu.cn。

 

 

本文作者：NCC lab 曲由之

校对：刘泉影、宋卓异

如需转载请先发邮件咨询：刘泉影，liuqy@sustech.edu.cn