2020年7月3日电子科技大学顾实教授受南方科技大学生物医学工程系刘泉影助理教授邀请，在生物医学工程系生物医学讲堂进行了题为《脑网络控制理论分析》的讲座。本文为该讲座的总结推文。

       本讲座中，顾实教授分别从研究动机、拟解决的问题、理论基础、临床应用等角度介绍了其团队在脑网络控制理论方面的多个工作。

 

1. 研究动机与科学问题

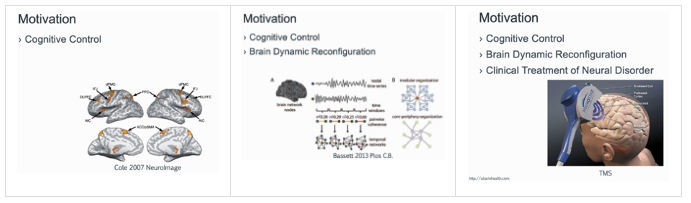
       对脑网络的控制的研究，主要有如下三个方面的动机：

       研究动机1是脑网络控制能用于认知控制(cognitive control)。认知控制是一个复杂的人类认知神经过程。在认知任务中，它涉及到认知状态的转换。之前的一些研究通过激活地图(activation map)的方法探究大脑哪些区域会牵涉（involve）到认知控制的过程中，但是这样的研究缺乏在神经机制上的解释。网络神经科学(network neuroscience)的发展则从网络的角度寻求解释：牵涉到的大脑hub区域是怎么参与到整个认知调控过程中。

       研究动机2是它能用于大脑动态重构(Brain Dynamic Reconfiguration)，即在静态结构的基础上，关注动态结构的转换。Bassett et al. (2013)通过研究在不同的时间窗口内动态脑网络连接结构的调整，发现网络拓扑结构可能是跟认知能力、认知过程等有关。动态重构大脑能揭示哪些脑网络模块化结构(module structure)发生了变化，从网络动力学模型的角度，而不是简单的从数据驱动的角度，对网络随时间的变化进行解释。

       研究动机3是脑网络控制能用于神经疾病临床治疗(Clinical Treatment of Neural Disorder)。在治疗精神疾病过程中，可能会采取脑刺激干涉的方法，比如利用经颅磁刺激技术(TMS)刺激大脑特定区域，以激活或者抑制某些脑区。现有的研究一般是基于经验规律选择某些区域施加信号，而通过网络控制理论构建区域间影响的研究范式，可以设计更优化的治疗方案，甚至一些试探性的结果。这些结果使得对神经反馈(neuralfeedback)、干预(intervention)从经验性方法上升为具有系统性理论保障的科学体系。

       基于上述3个研究动机，构建脑网络控制理论，以解答如下三个科学问题：

       科学问题1: 对脑网络的调控、动态网络调整、认知过程的状态转换(state transition)都需要考虑到一个最基本的问题，即如何去定义、表达大脑状态以及描述状态间的转换，如何使用连续、离散或其他方法把它与可测神经信息结合起来。

       科学问题2: 如何度量一个脑区对整个系统动态的影响：即如何从网络的角度，考虑整个神经系统的状态变化，及其所涉及的多个脑区间的联系；如何从理论出发，量化某种干预(intervention)在不同脑区的影响；如何去度量每个脑区对整体动力学的影响。

       科学问题3: 如何建立动力学模型与实际应用之间的联系，实现理论与实际相结合。

 

2. 脑网络与动态

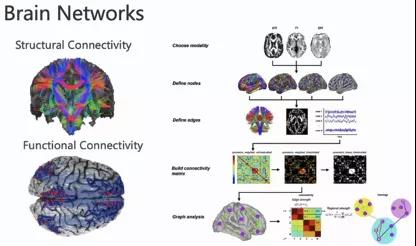
       脑网络基本构造分为两种，结构脑网络和功能脑网络。结构脑网络一般基于弥散张量成像（Diffusion Tensor Image, DTI）。功能脑网络一般基于功能核磁BOLD信号，或者基于电生理eeg、meg信号。

       在构建脑网络的过程中，首先对影像进行预处理，然后结合模板将大脑分成不同的区域。接着基于不同的构造边(edge)的方式把不同区域作为节点(node)，形成节点间的连接矩阵。对于DTI，使用的是构造性连接的数目、密度等等具体的指标。对于功能性脑网络，可以直接从时间序列出发开展相关性分析，得到脑网络图(graph)。构造脑网络图后，进一步结合图论(graph theory)的方法对图的网络性质进行研究。

       这里使用最一般的动力学方程来描述大尺度脑网络中大脑的状态(state)及其状态转换(state transition)。x(t)表示每个区域的状态信息，它的值可以是观测到的信号，比如说像BOLD信号。假设有n个区域，x(t)构成一个n*1的向量，它表征所研究系统在t时刻的状态。最简单的微分方程就是说把它的导数写成依赖于它当前状态的一个函数f。具体的建模依赖于怎么定义f。最简单f函数就是线性模型，复杂的f也可以是高阶模型等等。

       下面是一个简化的模型，它考虑了不同区域之间的相互作用，比如第i个区域它的导数依赖于自身的状态变化f_i。相互作用即不同区域对i区域的一个影响。tau_{ij}表示时间的延迟，W_{ij}表示两个节点间的权值，S表示非线性转移函数。对于具体功能的脑网络，我们需要推断系统的变换参数。对于结构脑网络，可以假设这个f_i可能的形式,W_{ij}则可能以某种形式依赖于它的连接状况。

       基于这个模型，可以开始尝试性的探究动力系统的过程。比如研究系统可控性、控制能量、系统干预(intervention)等。

3. 大脑控制模型与系统可控性和稳定性

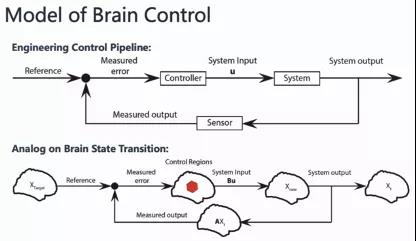
       从控制的角度出发，讲述如何对大脑网络进行控制。第一个图是经典的工程控制过程。为了维持系统的正常运行，从当前的状态校正到期望的状态。在每个时刻，通过测量系统状态信息与期望状态的误差，通过设计系统控制器，以降低误差的形式进行系统调控。第二个图是将类似的思想用于脑网络控制，例如对于大脑的状态转换的控制。比如任务状态切换、区域激活抑制或者区域信号加强等。大脑内部区域抑制某些区域的信号，通过把某些区域当做控制区域，信号从这些区域输入，从而影响整个大脑的激活状态；或者说连接情况的改变，使得大脑从当前状态转移到目标状态，从而实现认知控制的过程。

       那么怎么类比于工程控制的过程，用相应的控制论方法探究大脑不同区域对整体动力学的影响呢？下面介绍了一个简单的线性模型。

       这里列举了简单的线性、离散、无噪声动力学模型。假设t+1时刻的状态x(t+1)依赖于t时刻的状态转换A·x(t)以及相应的控制项B_K·u_K(t)。B_K是一个N*K矩阵，它表示在具体的状态转换过程中选择哪些区域作为控制区域。而u_K表征了在不同的时刻控制的具体形式。

       具体的建模中，对结构脑网络，我们最初假设A是与脑结构连接矩阵有一定关联性。具体的关联性可以转换成Laplace，或者说除以一个系数，只需要保证整个系统的稳定性。B_K的选择取决于感兴趣的区域。把它设置成认为的与控制过程相关的区域，或者之前实验验证的区域，或者设置成所有区域以探究整体系统的性质。具体来说，u_K就是在研究过程中，可以基于可建模的动力学系统进行优化的外界控制，或者从能量最低或者路径最短角度进行设计，基于这些限制可以求解最优的u_K。

       可控性(controllability)就是系统在给定外部输入，移动到目标状态的能力。如果每个状态都是可达的(reachable)，这个系统就是可控的。从纯理论上来说就是：系统能否在t步时间内达到目标状态。从最开始的线性方程，通过推导得到前面t-1时刻可能性的输入，也就是这里所写的C矩阵的公式。如果这里所记的C矩阵是一个满秩矩阵，不管前面的x_t, x_0怎么变，总能选取一定的u值，使得方程成立。

       系统的稳定性通过系统的同步性S进行度量，直观上理解这个度量指标就是特征值方差的倒数。公式中，d表示连接的平均强度，主要是用于正则化，消除掉边的连接强度因素。如果说特征值都靠的非常近，意味着大脑很容易就处于同一个模式(mode)。如果大脑都处于同一个模式，那么它整个状态的丰富性、灵活性都会受到比较大的影响，整体的效率(efficiency)也会下降。

       当我们要改变这个系统，系统的可控性涉及到需要多少能量。需要能量很少，意味着这个系统很容易改变，也即这个系统更容易被控制。这里描述的是一个T步的离散的过程。连续过程可以转换成积分形式。这里控制能量定义为每个时刻的u的2次方做累加，这是一种最直观的方式。当然也可以采集不同形式进行定义，比如添加正则化等。定义好控制能量之后，可以通过极小化控制能量，来求解出每个时刻的u_K。

4. 脑网络上的控制系统

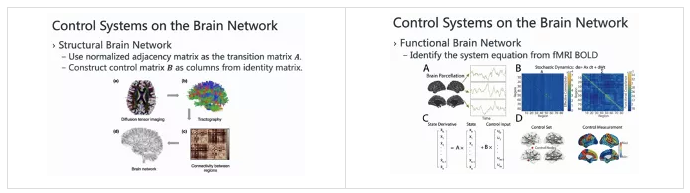
       脑网络控制目前主要从结构和功能两个角度进行分析。具体动力学过程都是从类似的线性方程出发。差别在于连接矩阵的定义，包括具体的状态转移矩阵A和控制矩阵B的设置。

       一是基于结构矩阵的分析。基于邻接矩阵，构造结构控制模型的A矩阵，我们使用节点的连接数目进行定义A矩阵，也可以使用流线(streamline)的密度(density)等等。如果有时间序列或者仅仅从结构出发，这种情况下B矩阵设为单位矩阵。

       二是功能脑网络分析。这个时候可以使用不同区域的时间序列的信号推断状态转移矩阵A，考察不同区域之间的关联性。从功能连接的角度，不同区域之间的时间序列具有一定相关性。这个相关性可能是从某种程度编码一些交互(interaction)的具体模板(pattern)。例如，构造一个随机的动力学过程，通过推断A和B的具体值，然后基于推断的区域间的方差矩阵和区域间的有效连接，构造基于功能时间序列的控制方程，探究它们的控制集或者控制量等关系。

5. 脑网络控制系统的可控性

5.1 可控性度量

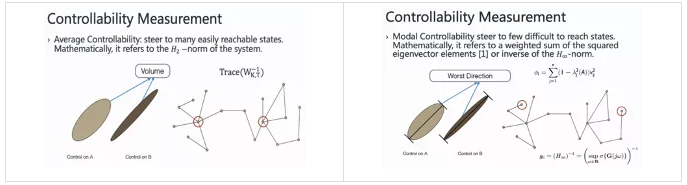
       这里介绍两种可控性度量方法，平均可控性(average controllability)以及模式可控性(modal controllability)。

       平均可控性主要是衡量单位能量下系统能达到不同状态的平均情况。也就是说，把一份能量放在哪些区域，平均来说它更容易影响到整个系统的变化。大家可以理解成，给定单位能量，能到达的状态的一个面积。在这种情况下，如果把这份能量放到连接边数比较多的区域，那么它就更容易影响其他相连接的区域。从平均的意义上，这些区域就是一个更有效的选择。

       而模式可控性，它考虑相对来说最坏的情况。系统遍历它所有可能的球面，最坏的情况就是某些状态会消耗特别多的能量。在这个策略下，希望控制能量在最坏的情况下要最好。也就是说，在比较偏的连接比较少的区域，如果把影响施加在连接比较强的区域，那么控制能量分散较少部分到比较偏远的区域。也就是说，在改变最坏情况的时候，能量消耗就相对比较大。希望最坏情况最好，比较直观的策略就是直接控制这些区域。

 

5.2 可控性地图

       这里展示了两种可控性的大脑地图(map)分布，即基于前面我们定义的度量，这两种可控性度量在大脑的具体哪些区域的数值比较高(红色)，哪些脑区比较低(深蓝色)。左边展示了基于结构脑网络，右边展示了功能脑网络的具体情况。

       可以发现两个脑网络的平均可控性是有区别的。整体数值比较高的区域都是连接比较强的。比如，结构脑网络，它倾向于去选择结构的hub，而功能脑网络倾向于选择功能的hub。基于这个策略，在默认网络中比较强连接的一些hub被选取为高效的控制节点。从某种程度上，解释了为什么在静息态下，默认网络的相对激活性会更高。因为相对常规的想法是在静息状态下，大脑处于相对低耗的状态，那么维持低耗的有效状态，就需要考虑在哪些区域影响整体使之更有效率。

       前面提到的一些最坏情况也就是需要能量更多的情况，即相对更复杂的任务。在执行这些任务的时候，对应的控制区域就是它们自身。像frontal-parietal区域，不管从结构脑网络，或者从功能脑网络，相对来说在模式可控性(modal controllability)数值上相对更高。某种程度上也就帮助大家理解为什么说这些相对弱连接的区域它们的功能会更细化，有些时候也会更特殊的辅助大脑执行复杂任务。

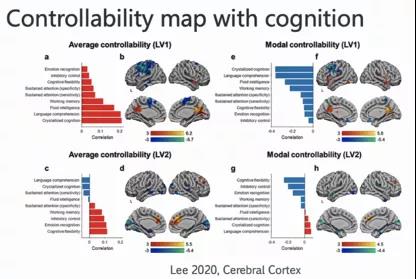
       这里用另一种方式展示大脑的可控性地图(controllability map)，它是定义的认知度量在大脑上的分布与认知区域的关联性。这里的LV1其实是用线性回归(linear regression)得到的一些变量(variables)，也可以理解成，用主成分分析方法看第一个主成分与第二个主成分可能覆盖哪些区域。可以看到，因为平均可控性涉及到整体平均的效率，所以和一些综合性指标，比如晶体认知(Crystallized Cognition)、流体智力(Fluid Intelligence)等综合性指标具有关联性。那么在这些关联的区域上，其可控性的差别能显示出个体差异(Individual Differences)。相应的在模式可控性，所定义的一些特征呈现负相关特性。

5.3 可控性的可靠性

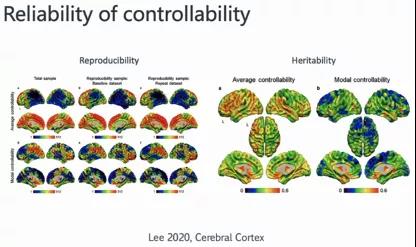
       在同一篇论文中，分析了另外两种度量：可重复(Reproducibility)和遗传性(Heritability)。

       左图表示在同一个项目中，通过扫描多次，针对基线(baseline)做可重复性的时候，观测控制性度量的分布，验证分布的一致性，判断是否是随机的过程。但是这很大程度依赖于它的连接情况，即连接结构的可重复性。

       右图反映了遗传性关系，观测遗传基因的表达，或者测量不同子代之间的亲代和子代之间的关联性。可以发现prefrontal的区域，在平均可控性上它的遗传性相对来说更高。而在模式可控性，遗传性更多的是在Pre-temporal和Supramarginal的区域，它可能是衡量可遗传的具体特征。

 

5.4 可控制之间关系

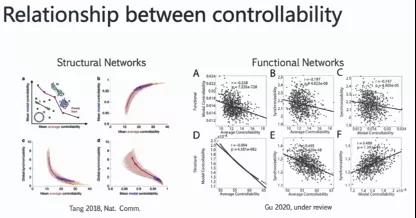
       平均可控性和模式可控性两个度量(average controllability and modal controllability)之间具有一定的关联性。这种关联性依赖于不同矩阵的选择。如何刻画这两个度量，可以通过：1)它们自身的直接关联；2)随着时间推移或者神经发育的具体过程，两个度量之间具体的tradeoff关系。随着年龄的增长，更多的是两个都有所增强，还是说一部分能力去抵消或者促进另一方面能力的发展。Tang 2018年的论文，具体描述了模式可控性和平均可控性之间的tradeoff关系，是一种Pareto最优的方法，平均可控性跟整体的同步性具有负相关性。但从个体考虑，对brain做整体值考虑，平均可控性与模式可控性两者是呈现正向相关，但不是单纯的线性关系。

       如果说不同区域有两种考察方法，一是对整个大脑定义一个具体的值(average across subject)，另一个是对不同区域(average across region)。在这两种情况下，它们间的关系是不太一样。在Gu et al.(2015)论文中也发现，如果在区域取平均，以及在样本空间取平均，考察两者之间的关系，两者呈现出很强的负相关区域。总结性的说，模式可控性的分布和平均可控性的分布呈现出很强的负相关。但是从整体考虑的话，就包括像前面的平均可控性和模式可控性的关系，就不是简单的线性关系。而在功能脑网络的控制分析，相应的情况就会更复杂。因为它涉及到连接转换矩阵以及控制矩阵，矩阵的选择不再是单位矩阵，它涉及到区域间的具体作用。

       不同的状态转移矩阵和控制矩阵的选择，会对两个度量之间的关系产生影响，它涉及到一些具体的设定，也就是说两个度量反映了脑网络上相应的拓扑性质，而这种拓扑性质是受到控制区域之间的关联，还有状态转移矩阵的影响。

 

5.5 可控性和图度量

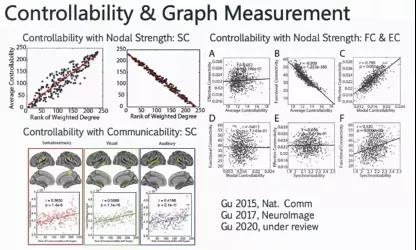
       这里探究说这两个控制度量跟传统度量(连接的度、communicability)之间的关联性。从结构的角度来说，连接性就是连接的度，就是把每个区域的连接情况，连接强度求和。平均可控性与连接的度呈现出很强的正相关，这是从样本空间上求平均得到每个区域的具体结果。

       communicability可以理解成是在脑网络上从一个区域到另一个区域，路径长度的加权平均。实验发现communicability与可控性呈现出较强的正相关。从控制的角度，信号的传播(propagate)是沿着脑网络进行，random walk也是沿着同样的脑网络信息。基于这样的假设，控制网络会有具体的路径设置和筛选。右图是在功能脑网络上做的实验，基于功能连接方式(functional connectivity)以及有效连接(effective connectivity)，实验发现基于有效连接，它与模式可控性呈现强的正相关，而平均可控性与功能连接有很强的负相关。

 

5.6 可控性的应用举例

应用实例1: 可控性预测任务表现

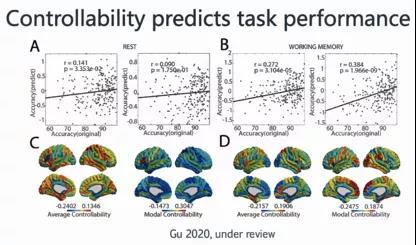
       上图讨论了我们定义的度量与实际应用的关联。检验的标准涉及到它们是否能预测感兴趣的东西以及发现临床上不同群体之间的差异。这里从静息态以及工作记忆(working memory)两个角度进行分析，研究发现，在working memory task它们的预测精度相对更显著，在静息态下则相对不显著。

       在具体的working memory task，我们可以发现平均可控性和模式可控性可以预测具体任务的分数。尤其在frontal和parietal脑区承担重要角色，从某个角度印证了这两个控制度量从某种程度确实是可以刻画大脑在认知任务的效率问题。

应用实例2:可控性标记双相情感障碍组

另一个例子，如果使用传统的度量标准，两组(Control group与bipolar disease)区分不显著。而采用平均可控性，control和bipolar disease两组呈现显著的差异。这从侧面印证了控制度量相对于传统的脑网络度量，具有更强的敏感性，是一种更灵敏的biomarker。

应用实例3: 可控性与TMS效果的关系

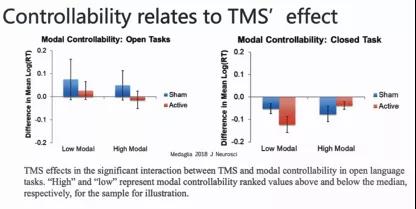
       这是在TMS’ effect上的研究。在低模式可控性(Low Modal Controllability)以及高模式可控性(high modal controllability)的大脑区域上分别进行TMS的干涉。

       在open language task中，在低模式可控性以及高模式可控性区域进行不同控制，呈现出不同的Log(RT),（RT: Response Time响应时间）。从某种程度初步验证了模型的可行性，因为在不同区域上的差异可进一步开展后续的研究，即如何去理解和利用这些差异。

应用实例4:控制能量鲁棒性区分轻度脑损伤

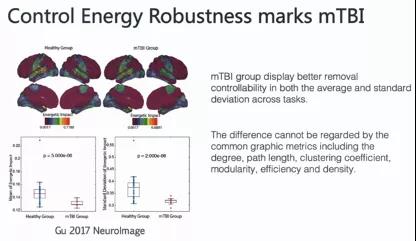
       这个工作是验证灵敏性指标，从控制能量的角度定义系统的稳定性。比如说把某些区域从整个系统中移除，那么控制路径以及控制能量也会发生偏差。移除不同区域产生不同的影响，通过对整体求平均从某种程度上刻画系统的稳定性。

       这个工作是基于轻度脑损伤mTBI(mild Traumatic Brain Injury)进行验证。使用控制度量，healthy group与mTBI group具有非常显著的统计差异。而使用传统的度量方法，比如度(degree)或者路径长度，聚类系数等等一些指标，就无法体现出这两组之间的统计差异。在具体的状态转移过程中，把相应的指标转换成能量指标，相对来说会更敏感及显著。如果可控性指标作为大脑整体的指标考虑的话，相当于从能量角度进行更灵敏的刻画，而不是简单的从connectivity关系的一个重复。

应用实例5:可控性支持神经发育

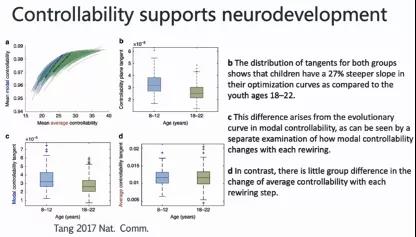
       这个研究证明了可控性与神经发育的关系。结合图a和图b来看，在不同年龄段，发展的一个趋势是由变化，即tangent斜率决定的，在8到12岁和18到22岁，它们的tradeoff关系不是线性的。图c和图d为不同年龄段的平均可控性与模式可控性的tagent。平均可控性相对来说是一个线性变化。而模式可控性表示执行复杂任务，它的变化是一个非线性的过程。从8到12岁和18到22岁的发育过程，对于复杂任务的处理或者相对复杂任务的发育，呈现出非匀速的过程。平均可控性的tangent在两组之间相对没有差异，也就是说青春期之后的大脑的过程，可能涉及到两个度量之间的tradeoff，对复杂任务和平均任务来说，更多的是平均发育过程。

应用实例6: 可控性支持认知

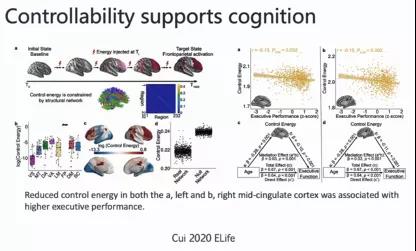
       这个图是Cui et al. elife(2020)的工作，它基于控制能量的角度，描述具体的认知任务中控制能量的关系。右图表示控制能量越低，任务的执行表现越好。这个与最初的观点一致，即控制能量低表明效率高，网络的控制效率高。相应的我们就猜测执行认知任务的效率也会更高。下面的调解分析(mediation analysis)支撑这个结果。

6. 未来发展方向

1.首先是把动态过程从线性到非线性的一个延拓。大脑是个非常复杂的非线性系统。如何比较好的平衡模型的复杂性及可研究性之间的关系，进一步通过构造相对合适的非线性模型刻画大脑的可控性。

2.针对功能脑网络，功能脑网络并不是一个stable的过程，如何添加temporal信息，并且在没有interaction的时候，如何去考虑外界随时间变化的信号，对刺激、对大脑的影响。

3.在具体的临床应用，针对健康人群或者疾病人群诊疗，我们需要设计科学有效又安全的干预方案，进而影响大脑动态，调控大脑的神经回路。并在实际应用中，验证和应用所提出来的理论假设。

 

Q & A

Q1:请问使用不同时间分辨率重构出来的神经动力学系统的特征一致吗？

A1:这个问题取决于你是否做temporal model。如果说就像我们刚刚所说的，其实是相对把连接做static的过程。在这种情况下，我们也试过使用不同的时间序列，得出来的结果相对比较稳定。因为很大程度上是对effective connectivity还有noise covariance的估计。如果说时间分辨率对这两个的估计不产生影响的话，那么推出来的结果它其实就比较稳定可靠。

 

Q2:请问controllability指标的灵敏度如何，能否与复杂的认知实验设计相结合？

A2:这个是比较好的问题啊。根据我们之前和后面介绍的研究。不管是working memory，还有一些与结构相关的mTBI等等的指标。我们的经验是，跟认知还有整个系统的特征相关的性质、相关的能力上还是比较灵敏的。但是具体的复杂认知实验，因为实验设计这块不是我的专长。我觉得如果这些任务跟整体性有关的话，相对应该是会比较敏感的。

 

Q3:controllability指标在不同意识状态下是否会一样的。比如说麻醉状态或者昏迷状态。

A3:比如说它的一些指标，它本身也是要从信号角度出发。如果你所感兴趣的信号。在这两种状态下，呈现出差别，那么我们要问的问题是说controllability是否能从系统动力学的角度，或者从控制的角度去阐述系统的控制性。在这两种状态下是否有差别。如果说有差别，那么我们希望是这个指标，这个方式能去刻画。而如果定义的某种东西可能只是跟纯结构的关联性。那么，在麻醉或者说昏迷状态下，它的结构本身不发生变化。那么这个指标当然也不会发生变化。而如果你感兴趣的一些功能信号的具体的pattern发生了变化，那么这个pattern如何去影响系统的一些控制性。那么这是一个可以研究和探究的内容。

 

Q4: controllability这些指标是针对每个被试有个单个的数值，类似于度聚类系数这样的吗？

A4:这个是可以的，就是你刚刚所说，你一方面把它具体算出来的话，像我们所谓average controllability，还有一些modal controllability这两个指标的话，每个个体，每个区域都是有一个值，然后你可以考虑到一些群体效应，既可以在subject level去求平均，也可以在region level去求平均。就是说，每个个体得到一个值，或者说每一个区域得到一个值，都是可以。

 

Q5:这套方法在eeg或者meg上应用是可行的吗？

A5:是可以的，我们这边有个合作方(Scheid, B. H. 2020)，他们做的是利用可控性去探究癫痫的一些性质，用的是eeg还有ecog的信号。

 

Q6:您使用到的指标，观察过结构网络连接和功能网络连接的关系吗？

A6:我们之前有过一个工作。那个不是从控制角度出发，因为那个是从纯能量角度去构造的一个随机模型。就是说你可以从结构出发去预测功能。然后这里模型也是类似的啊。就是比如说你去刻画它的状态转换，就是基于结构去刻画它的状态转换，符合hemodynamic的过程，然后去预测功能连接，你就说通过这个模型去探究结构与功能之间的similarity，这样是可以的。

 

Q7:能否量化脑网络中加工中的自动化加工。神经信号活动本身的variability是否属于controllability的范畴。

A7:这是一个比较好的问题啊。但是这个具体去做的话可能涉及到一些具体的定义问题。就比如说神经活动本身的variability，这个variability是否涉及到它本身，而网络controllability的一些变化。比如说不同神经活动，它从连接上，或者说从时间序列在某段区域的变化，当然都是有区别的。那么从controllability的角度去阐述这个variability也是非常有意思的方向。这块工作我目前还没有做过，但是这个问题我觉得很有意思。

 

Q8:请问可控性度量和网络度量的相关性说明了什么问题呢？

A8:他其实就是可靠性度量，尤其是比如说回到结构那个地方，我们其实可以看出来，他很大程度上是基于连接去定义了这么一个度量。因此其实它跟网络度量的一些相关性其实是相对比较可预测的结果。然后这里展示了他的一些关系，主要也是相当于去帮助大家理解它可能会是跟哪些网络度量，哪些跟传统网络度量之间可能会有一些什么联系。比如说像跟communicability，就是刚刚举得一个例子，communicability它相当于去刻画random walk，可是相对于比较random的信号的propagation。而control的话其实相当于说你有规律的去控制它的propagation，那么这两者之间就是，有什么差异性或者说有什么关联。主要是辅助理解，可控性度量跟传统网络度量的关联和差异。倒也不是为了说明什么具体的问题，也不存在是谁诱导出了谁的关系。

 

Q9:首先是为什么做结构网络的可控性研究，选用的是DTI这个模态啊，还有其他的模态吗？第二个问题是做功能网络的可控性研究，对时间序列的长度有要求吗？现在常用的时间长度是怎样的？

A9:为什么选用DTI这个模态，因为我们一般做结构网络的话，你要有结构连接，然后结构连接DTI或者说DSI等等是比较常用的刻画区域和区域之间结构性连接的方式。所以我们就选用了DTI这个模态，然后功能可控性的话对时间序列的要求，我们之前用的是HCP的数据，时间序列长度还是有一定要求。因为时间序列过短的话，去估计noise covariance是没有什么问题，但是去估计effective connectivity问题的时候。在时间序列短的时候会很不稳定。最起码你的长度肯定是要比你的区域多。比如说，划分90个区域，你时间序列的长度200左右应该就没有什么问题。

 

Q10:功能可控性反映的是灰质类的信号，而DTI是白质。这样的话可能没有办法做一个比较。

A10:一般我们也没有去直接比较功能和结构可控性的特征。但是， DTI的白质其实也是你可以理解成他是上面那些灰质区域的一个连接，灰质区域一方面它本身有一些近距离的连接情况，但另一方面它也有一些通过白质的连接。所以你不能说这两个之间的信号就是完全独立开来。这也就是大家去研究结构和功能连接关系的同样的出发点。但你可能说去单纯比较它的可控性，也不能说完全就没法去做一个比较。因为出发点也是一样的嘛。就是说那些灰质区域它的一些连接跟白质不是一个独立的东西。

Q11:是否已经有比较方便的工具可以做这一类的控制分析。

A11:Bassett教授的网站上，他们分享的一些代码是我写的，有一些就是跟控制相关的一些工具。大家可以去他们那个网站上找。然后我们的话我前阵子也做了一个相关于论文的一个collection，我回头分享到群里面。大家感兴趣的话。可以去根据另一个论文的collection去找一些大家感兴趣的部分读一下。

 

Q12:能否找到一个指标去量化脑网络中的自动化加工。就是这个自动化加工，我个人的一个理解就是比如说你在静息状态下，他其实更多的是一个自发性的，比如说spontaneous activity或者是他是一个反应内在的，而不是说你是有意识去控制的这样一种活动。所以就比如说包括决策过程中，他有很多就是说bias。然后这个可能是自下而上的，或者说从subcortical到cortical的一个自下而上，或者是从情绪诱发的这样一种就是区别于纯粹的一个认知活动，就是里面可能包含了这一部分信息。然后我就是想知道就是说能不能有这样一个指标。因为controllability他是你可能更多的是跟自上而下的这样一种活动有关。那有没有一个指标可以量化，这种就是自下而上的这种活动。然后因为我看到就是说您那个就是用controllability去预测它的那个resting state那个activity他的效果不是很好，因为静息状态下，它更多的是一种自发性的一个信号。所以我觉得这可能是一个原因之一。

A12:我觉得这个点挺好啊。然后我再稍微说一下那个地方我们是拿静息态去刻画它的一些任务的执行情况。这个可能是有这方面的原因。您刚刚也说了，静息态可能是说涉及到一些自发性的，不一定涉及到它具体任务的执行的效率。那么自发性的去预测它整体效率的执行，就相对可能不是一个feasible的事情。但是controllability度量本身就不管用，从结构可控性还是功能可控性。就是从功能可控性的角度来说，他对静息态和功能态两个本身其实是非常明显的。但只是今天做slides的时候，就是没有去把这一块作为一个特征给他放出来。我们那个论文里面，我们已经挂在arxiv (Deng, S. (2020))，然后是可以看到里面也列了它在对静息态还有功能态本身的区别。

 

 

顾老师推荐：

1. Must-read papers on Brain Control Analysis

https://nangongwubu.github.io/posts/2020/06/blog-post-3/

 

2. Controllability of Structural Brain Networks Toolbox:

https://complexsystemsupenn.com/s/controllability_code-smb8.zip

 

 

参考文献：
Cole, M. W., & Schneider, W. (2007). The cognitive control network: integrated cortical regions with dissociable functions. Neuroimage, 37(1), 343-360.
Bassett, D. S., Wymbs, N. F., Rombach, M. P., Porter, M. A., Mucha, P. J., & Grafton, S. T. (2013). Task-based core-periphery organization of human brain dynamics. PLoS Comput Biol, 9(9), e1003171.
Tang, E., Giusti, C., Baum, G. L., Gu, S., Pollock, E., Kahn, A. E., ... & Gur, R. E. (2017). Developmental increases in white matter network controllability support a growing diversity of brain dynamics. Nature communications, 8(1), 1-16.
Lee, W. H., Rodrigue, A., Glahn, D. C., Bassett, D. S., & Frangou, S. (2020). Heritability and cognitive relevance of structural brain controllability. Cerebral Cortex, 30(5), 3044-3054.
Tang, E., Giusti, C., Baum, G. L., Gu, S., Pollock, E., Kahn, A. E., ... & Gur, R. E. (2017). Developmental increases in white matter network controllability support a growing diversity of brain dynamics. Nature communications, 8(1), 1-16.
Deng, S., & Gu, S. (2020). Controllability Analysis of Functional Brain Networks. arXiv preprint arXiv:2003.08278.
Gu, S., Pasqualetti, F., Cieslak, M., Telesford, Q. K., Alfred, B. Y., Kahn, A. E., ... & Bassett, D. S. (2015). Controllability of structural brain networks. Nature communications, 6(1), 1-10.
Gu, S., Betzel, R. F., Mattar, M. G., Cieslak, M., Delio, P. R., Grafton, S. T., ... & Bassett, D. S. (2017). Optimal trajectories of brain state transitions. Neuroimage, 148, 305-317.
Jeganathan, J., Perry, A., Bassett, D. S., Roberts, G., Mitchell, P. B., & Breakspear, M. (2018). Fronto-limbic dysconnectivity leads to impaired brain network controllability in young people with bipolar disorder and those at high genetic risk. NeuroImage: Clinical, 19, 71-81.
Medaglia, J. D., Harvey, D. Y., White, N., Kelkar, A., Zimmerman, J., Bassett, D. S., & Hamilton, R. H. (2018). Network controllability in the inferior frontal gyrus relates to controlled language variability and susceptibility to TMS. Journal of Neuroscience, 38(28), 6399-6410.
Cui, Z., Stiso, J., Baum, G. L., Kim, J. Z., Roalf, D. R., Betzel, R. F., ... & Ciric, R. (2020). Optimization of energy state transition trajectory supports the development of executive function during youth. Elife, 9, e53060.
Scheid, B. H., Ashourvan, A., Stiso, J., Davis, K. A., Mikhail, F., Pasqualetti, F., ... & Bassett, D. S. (2020). Time-evolving controllability of effective connectivity networks during seizure progression. arXiv preprint arXiv:2004.03059.

 

讲座观看地址：

https://www.bilibili.com/video/BV1kk4y1q7vB?from=search&seid=8807585475690151569

 

写作：梁智超

校对：顾实、刘泉影

编辑：王海慧